Öntanuló rendszer alkalmazása a hajtásvezérlésben

Kérlek válassz a bal oldali menüből!

Beszámoló

A 2021-2022. években az Óbudai Egyetem Kandó Kálmán Villamosmérnöki Karán végzett kutatásom feladata öntanuló rendszerek alkalmazásával működő automata fokozatváltót vezérlő (TCU) eljárást készíteni. A cél az, hogy egy, az emberi vezető döntéseit modellező rendszer jöjjön létre, tehát olyan paramétereket kell figyelembe venni, amiket egy ember képes megállapíteni, mint például egy kanyar lehet enyhe vagy éles, a következő útszakasz belátható vagy beláthatatlan stb.

Kutatásom célja, hogy egy döntéshozó rendszer modelljét megtervezzem, ami az emberi vezető döntéseit modellezi, a számára is elérhető információkat figyelembevéve, annak érdekében, hogy az intelligens, öntanuló módszereket is alkalmazó vezérlő a fokozatváltás időzítésével és a megfelelő fokozat kiválasztásál javulást érjen el a hajtáslánc energiahatékonyságában. A kutatás alapgondolata, hogy a villamos motor nyomaték-sebesség diagrammjában a legmagasabb hatásfokon kell tartani a munkapontot a szükséges nyomaték előállítása mellett a nyomatéktartalékot biztosítva a megfelelő járműdinamika elérése érdekében.

A tervezett rendszer a saját pozíciójának ismeretében lekérdezi online adatbázisokból a környezetében fellelhető és az útvonal terv szerint érintett kanyarokat, tengerszint feleti magasságokat, amik felhasználásával az útviszonyok és a vezetői stílus alapján megbecsüli a szituációhoz leginkább illesztkedő sebességet és fokozatot.

A kutatási terv szerint 10 hónap áll rendelkezésre a probléma megoldására vagy a tézis cáfolására. Minden egyes mérföldkőnél bemutatásra kerülnek az addig elért eredmények és felvázolásra a további ötletek.

Az első beszámoló az IEEE CANDO EPE 2021. konferencián került publikálásra és bemutatásra az alábbi DOI és MTMT azonosítókkal ellátva.

• Study of vehicle dynamic properties and gear shifting mechanism of electric vehicles
• DOI: 10.1109/CANDO-EPE54223.2021.9667815
• MTMT: 32586881

A XXXVII. Kandó Konferencián került először bemutatásra a keresőablak, mely a TDK dolgozatban részletesebb elemzésen is átesett. Ez szintén regisztrálásra került a Magyar Tudományos Művek Tárának adatbázisába a következő azonosítóval:

• Menetrend szerint közlekedő buszok menetciklusainak tanulmányozása az intelligens váltásvezérléssel elért energiahatékonyság növelésének érdekében
• MTMT: 32640193

A következő dokumentum az OE-KVK kari TDK pályamunka formájában jelent meg, a Menetciklusok és kanyarodások elemzése fokozatváltással elért hatékonyság növeléséhez címet viseli. A pályamunka a 54. Tudományos Diákköri Konferencián (TDK) I. helyezést ért el és ajánlást kapott az országos fordulón történő megmérettetésre, melyre 2023. tavaszán kerül sor. A fő témája a TDK dolgozatnak a fokozatváltó típusok áttekintése, az adatgyűjtések módszere és a keresőablakot alkalmazó módszer bemutatása, lehetőségeinek elemzése. Ennek a pályamunkának a kísérő előadása megtekinthető az alábbi videóban:

A videó megtekinthető YouTube-on is.

A második félévben is készült TDK munka Modellezett villamos hajtáslánc alkalmazása megerősítéses tanítás környezeteként címmel, mely közel 75 ezer karakterében bevezeti az olvasót a villamos hajtáslánc típusaiba és ezek szoftveres és hardveres architektúráiba egyaránt. Ismertetésre kerülnek a hajtás részegységei, fontosabb számításaik és a teljes hajtáslánc hatékonyságának meghatározáásra is mutat be módszert. Szóba kerülnek még az alternatív hajtások lehetőségei is, melyek társíthatóak villamos hajtással, melyekhez a legfrissebb kutatási eredmények is lehivatkozásra kerültek.

A pályamunka a 55. Tudományos Diákköri Konferencián (TDK) az elsőhöz hasonlóan sikert aratott: I. helyezést ért el és ajánlást kapott az országos bemutatásra. Kísérő előadás az alábbi videóban:

A videó megtekinthető YouTube-on is.

A két TDK dolgozat egy közös előadásban meghívott előadásként bemutatásra került a Temesváron megrendezett "Határon túli" XXIII. MTDK-n is.

Előadás a Temesváron megrendezett 'Határon túli' XXIII. MTDK-n

Mindkét TDK munka 1. helyezést ért el az intézeti fordulán és a bírálók az országos fordulón bemutatásra is javasolták. Ezért a dolgozatok már feltöltésre kerültek az OTDT rendszerébe, jövő tavasszal ismét versenyeznek.

Első helyezett oklevelek

Ismertető

Bevezetés

Társadalmunk működéséhez elengedhetetlen a tömegközlekedési eszközök használata. Az emberek iskolája vagy munkahelye és az otthona között napi szintű ingázása akár több városon átívelő útvonal, melynek megtétele növeli életvitelének ökológiai lábnyomát. A konvencionális, fosszílis forrású üzemanyagot elégető technológia használata során a lelőhelyen történő kitermeléstől kiindulva a felhasználás során a mozgási energia eléréséig több állomáson keresztül történik az alapanyag feldolgozása átalakítása (well-to-wheel), így a járulékos vesztesége 86-91%. Ezzel szemben az elektromos hajtást használó járműveké 58-68%, amibe már a szállító elektromos hálózat veszteségei is bele vannak számolva. [d.01] Ígéretesen hangzik már a -18% veszteség csökkenés, viszont ahhoz, hogy érdemes legyen olcsón, sorozatgyártásban előállítani villamos járműveket a fogyasztóközönség számára, még rengeteg megoldásra váró probléma fennáll, hogy a világ mérnökei megoldják őket.

A kutatás előzménye és célkitűzése

Pályázatomat megelőzte az „Intelligens járműhajtás vezérlőrendszerének kutatása”. Ebben a projektben kifejezetten az ikerhajtással rendelkező menetrendszerint közlekedő buszokkal foglalkoztunk, de voltak ötletek, melyek nem feltétlen illettek a buszok témakörébe, ezért egy önálló kutatásba lettek kiszervezve, és ezek kerültek kidolgozásra az UNKP projekt keretein belül. A kutatás alapgondolata, hogy a villamos motor nyomaték-sebesség diagrammjában a legmagasabb hatásfokon kell tartani a munkapontot a szükséges nyomaték előállítása mellett a nyomatéktartalékot biztosítva a megfelelő járműdinamika elérése érdekében.

Elektromos járművek

Az elektromos járművek kifejezést a köznyelv gyakran összemossa a hibrid járművekkel. A tisztán elektromos járművek olyan belső égésű motor nélkül közlekedő járművek, amelyek a meghajtásukhoz szükséges energiát beépített akkumulátorból vagy más energiatároló eszközből nyerik, majd a tárolt elektromos energiát mozgási energiává alakítják át. A hatótáv körülbelül 150 és 450 kilométer között lehet, ami távolság megnövekedhet, ha elegendő mennyiségű nyilvános töltőállomást érint az útvonal, viszont minden töltésre fél órás pihenőt érdemes kalkulálni az útvonal megtervezésekor. Emiatt a gyártók az elektromos meghajtást más erőforrásokkal is kombinálják. Az elektromoson túl konvencionális motor is helyet kap a motortérben. Ezeket hívják hibrid járműveknek. Sokféle hibrid megoldás létezik, kezdve azzal, hogy a belső égésű motor csak áramot termel, vagy a meghajtásban játszik szerepet. Egy másik megközelítés, hogy csak magában a jármű képes megtermelni a szükséges energiát, vagy villamos hálózatra csatlakoztatható. Általánosságban elmondható, hogy ezek a járművek képesek regeneratív fékezésre, ami során a jármű újrahasznosítja a mozgási energia egy részét, úgynevezett rekuperációt végez, ami a hatótávolság növekedéséhez vezet.

Egy elektromos jármű felépítését két szempontból is érdemes megfigyelni a mozgásának csak 1 dimenzióra szűkített vizsgálatához.

A hardware szemszögéből 4 alrendszer különböztethető meg:

• hajtáslánc, ami a motortól kezdve a kerekig terjedő rendszer együttes megnevezése;
• nagy feszültségű akkumulátor, ami az elektromos energiát tárolja és szolgáltatja;
• jármű test, aminek megmozgatása a cél, továbbá amire a környzetből adódó erők hatnak;
• fékrendszer, amelyek a rendszer belső korlátozó erőit szabályozzák.

Villamos hajtás hardveres architektúrája

A vezérlő software szempontjából 5 alrendszert érdemes megemlíteni:

• Electric Machine Control System (EMCS), ami az inverter és a motor / generátor kezelésért felelős;
• Stability Control System (SCS), ami méri a jármű sebességét, erről és fékezésről szolgáltat információkat a többi alrendszer számára.
• Battery Management System (BMS), ami az áramellátást szabályozza,
• Driver Mode System (DMS) szolgál összeköttetésként a jármű és a vezetője között,
• Vehicle Control System (VCS) pedig fő vezérlője a járműnek, figyelembe veszi az előző 4 alrendszer által szolgáltatott adatokat, döntést hoz és rajtuk keresztül irányít.

Fontosabb vezérlőegységek jelei

Hajtás elemei

MATLAB Simulink Simscape hajtáslánc modellje

A képen a hajtáslánc modellje látható, az elemi műveleteket vagy épp alkatrészeket reprezentáló blockokat alrendszerekbe gyűjtve egy magasabb absztrakciós szinten figyelhető meg a szimulált környezet működése. A tápegység ellátja a motorvezérlőt árammal, mely meghajtja a villamos gépet motor üzemben, ez gép villamos energiából forgó mozgási energiát állít elő, mely egy sorosan kapcsolt nyomaték szenzorral és egy párhuzamosan kapcsolt elfordulás érzékelővel mérésre kerül. A forgó mozgás továbbításra kerül a fokozatváltóba, mely ebben az esetben egy diszkrét értékeket felsoroló állítható áttétel, annak érdekében, hogy a vizsgált eljárások hatását lehessen vizsgálni anélkül, hogy a vonóerő megszakításra kerülne. A kijövő tengely pedig a gépjárműtest szimulációjába érkezik, ahol a forgó mozgási energia hosszanti elmozdulássá alakul, mely szintén mérésre kerül, ismét menetciklusokat előállítva.

Áramforrás

Az oldal tartalmának feltöltése folyamatban van.
Kérem látogasson vissza később!

Akkumulátor

Inverter

Inverter egyszerűsített kapcsolási rajza

Üzemanyagcella

Protonáteresztő membrános üzemanyagcella működési elve; cella-sor szerkezete

Motorvezérlő

Az MCU feladata, hogy a vezető által kiváltott pedálmozgás alapján szabályozza a villamos gép meghajtását. Az alapján, hogy a járműt épp gyorsítani vagy lassítani kell eldől, hogy az EMCS-en keresztül az MCU által kezelt eszköz motorként vagy generátorként viselkedik a rendszerben.

Villamos hajtás szoftverének állapotgépe

Az fenti ábrán a VCS működésének egy egyszerűsített folyamata látható. Indításkor az inicializáló állapotba kerül. Feltételezve, hogy a járműhajtásának engedélyezése a jármű álló állapotában történik, az egyetlen állapotátmenet a gyorsító állapotba vezet, ha csak a gázpedál van valamennyire lenyomva. Gyorsítás állapotban alapértelmezésként a Névleges alállapot az aktív, ami azt jelenti, hogy nincs érvényben nyomaték- vagy teljesítménykorlátozás. Ha nincs lenyomva az egyik pedál sem, akkor a jármű csak a kinetikus energiáját használja a mozgásra. Ilyenkor a villamosgépen 0 Nm nyomaték kerül beállításra. Fékezés igényére a Rekuperációs állapotba kerül a rendszer, ilyenkor a villamosgép generátor üzeme működik. Az ellentétes irányú nyomaték elosztható az első- és a hátsótengelyek között. [o.07]

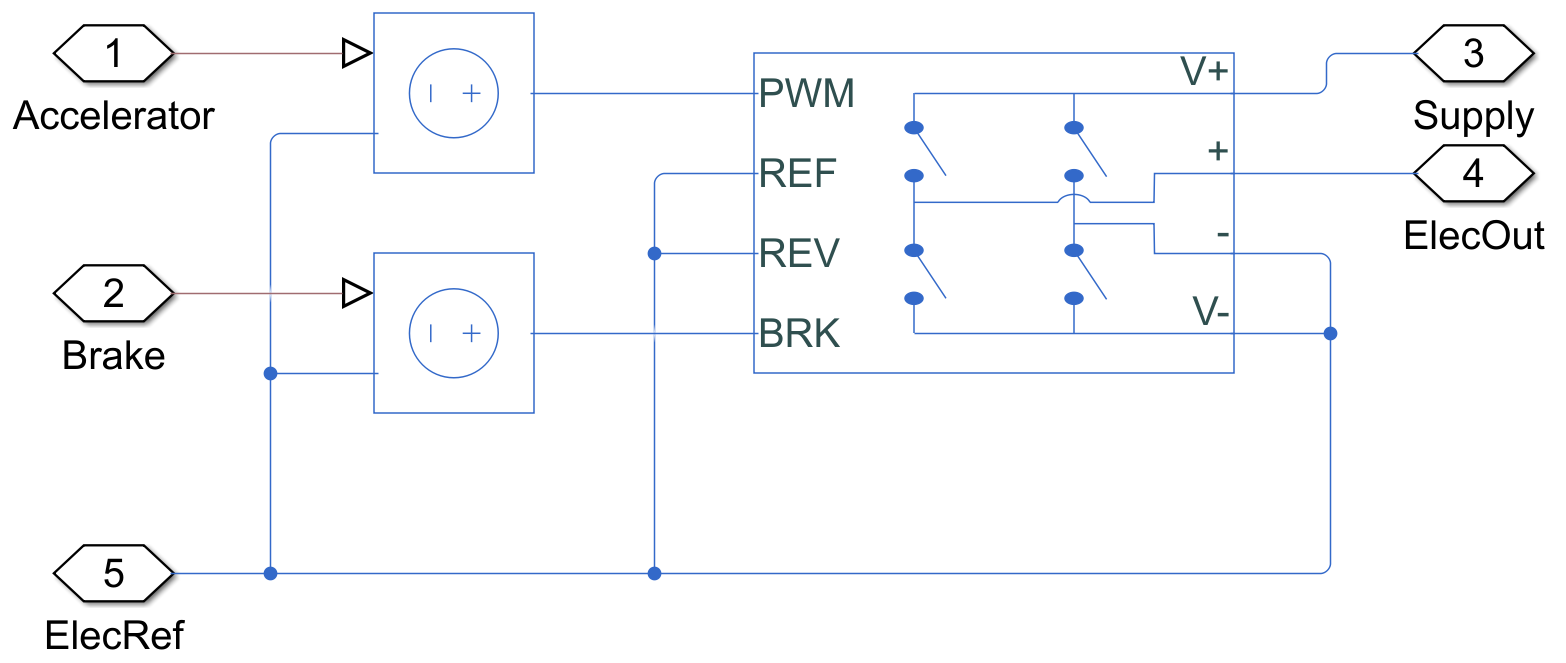
Motorvezérlő áramkör modellje

A motor vezérlésére egy külső H-híd került felhasználásra. Külső energiaforrásos üzemmód lett beállítva, hogy legyen lehetőség a modellben az akkumulátor vagy az üzemanyagcella szimulációjára és elkészülte után a rekuperáció is mérhető legyen. A vezérlés bemenetként a gázpedál és a fékpedál lenyomottságának %-os értékéből képzett PWM jelet fogadja, az ábrán szereplő két átalakító elem egy-egy szabályozható ideális feszültségforrás.

Villamosgép

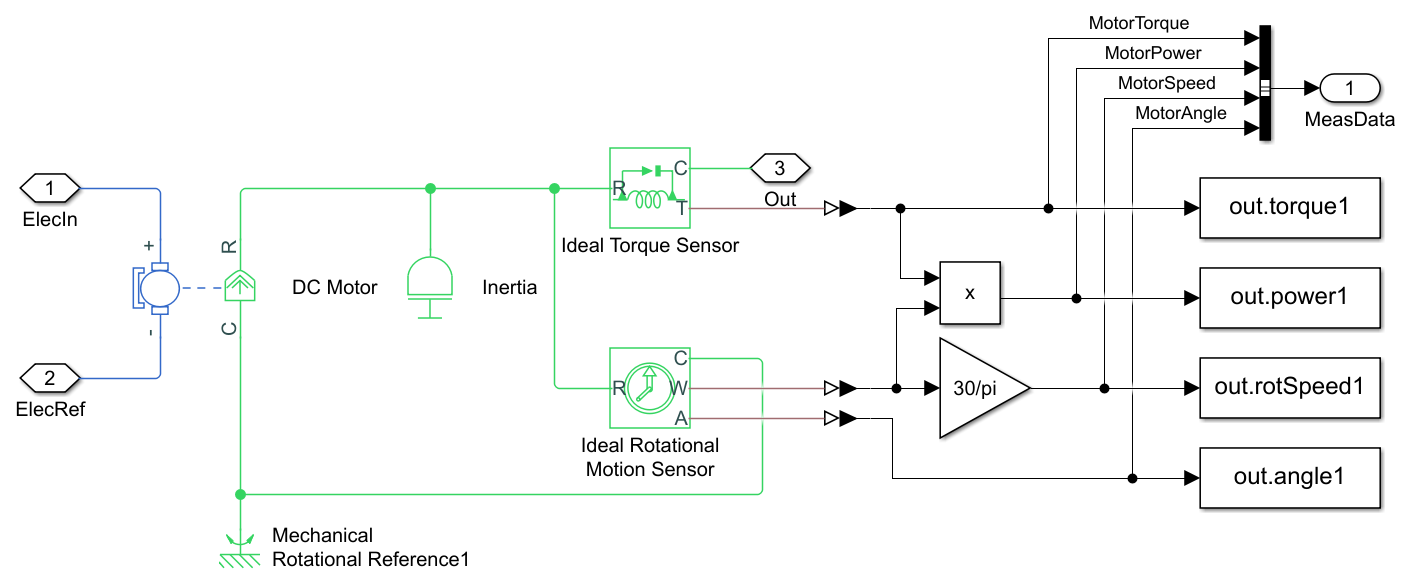
Motor modellje és mozgásának mérése

Az elektromotor alrendszerének modelljén az elektomechanikus átalakító mellett egy terhelés szerepel, az Inertia a jármű tehetetlen tömegéből adódó perdületet hivatott modellezni. Az alrendszer kimenete mérésre kerül egy ideális nyomaték- és egy ideális forgó mozgás szenzor segítségével. Érdemes megyfigyelni, hogy összeköttetésre kerültek és egy mechanikai rögzített pontra lettek huzalozva, tehát a motor álló része rögzítve van a szenzor álló részére, így azonos fordulatszámon pörög mind a két berendezés. A szögelfordulásból és a nyomatékból meghatározható a teljesítmény és a forgási sebesség is. A vonóerő átvitelbe sorosan közbeiktatott nyomatékszenzor után a sebességváltó következik.

Jármű dinamika

A jármű mozgása a rá ható erők és nyomatékok összesített hatásának eredménye. A gumiabroncs hosszanti erői előre vagy hátra tolják a járművet. A jármű tömege (m ⋅g) a jármű súlypontjában hat. A dőlésszögtől függően a súly a talajhoz húzza, és előre vagy hátra mozgatja a járművet. Bármely irányba halad a jármű, az aerodinamikai légellenállás lassítja.

1 szabadságfokú vektorábra: Járműtestre ható erők

A vonóerő, a súrlódási erő, az út meredekségéből és a légellenállásból adódó erők meghatározása a következő egyenletrendszer szerint történik:

\[ \begin{equation} \begin{gathered} F_{vonó} = \frac{M_v}{r_{dk}} = \frac{M_m \cdot i_v \cdot i_d \cdot \eta}{0,98 \cdot r_{sk}} \\ F_{aero} = \frac{\rho \cdot \beta \cdot A \cdot \overline{v}^2}{2} \\ F_{nyomó} = m \cdot g \cdot \alpha \cdot \cos{\theta} \\ F_{lejtő} = m \cdot g \cdot \sin{\theta} \\ F_{súrl} = m \cdot g \cdot \mu \cdot \gamma \end{gathered} \end{equation} \] ahol

• \( M_m \): a motor kifejtett nyomatéka,
• \( i_v \): a váltóval kiválasztott áttétel,
• \( i_d \): a differenciálmű áttétele,
• \( \eta \): a teljes hajtáslánc hatásfoka,
• \( r_{dk} \): dinamikus kerék sugár,
• \( r_{sk} \): statikus kerék sugár,
• \( m \): jármű össztömege,
• \( g \): gravitációs gyorsulás,
• \( \theta \): út meredeksége,
• \( \rho \): levegő sűrűsége 20°C-on,
• \( \alpha \): útterhelés eggyüthatója,
• \( \beta \): alaktényező,
• \( \gamma \): tengely terhelési együttható,
• \( \mu \): súrlódási-tapadási együttható.

A fenti egyenletek figyelembevételébel felírható a jármű sebességének képlete:

\[ a = \frac{\sum F}{m} \Rightarrow v = \frac{1}{m} \cdot \int (F_{vonó}-(F_{nyomó}+F_{lejtő}+F_{aero})) dt \]

Járműtest és erőátviteli rendszerek modellje

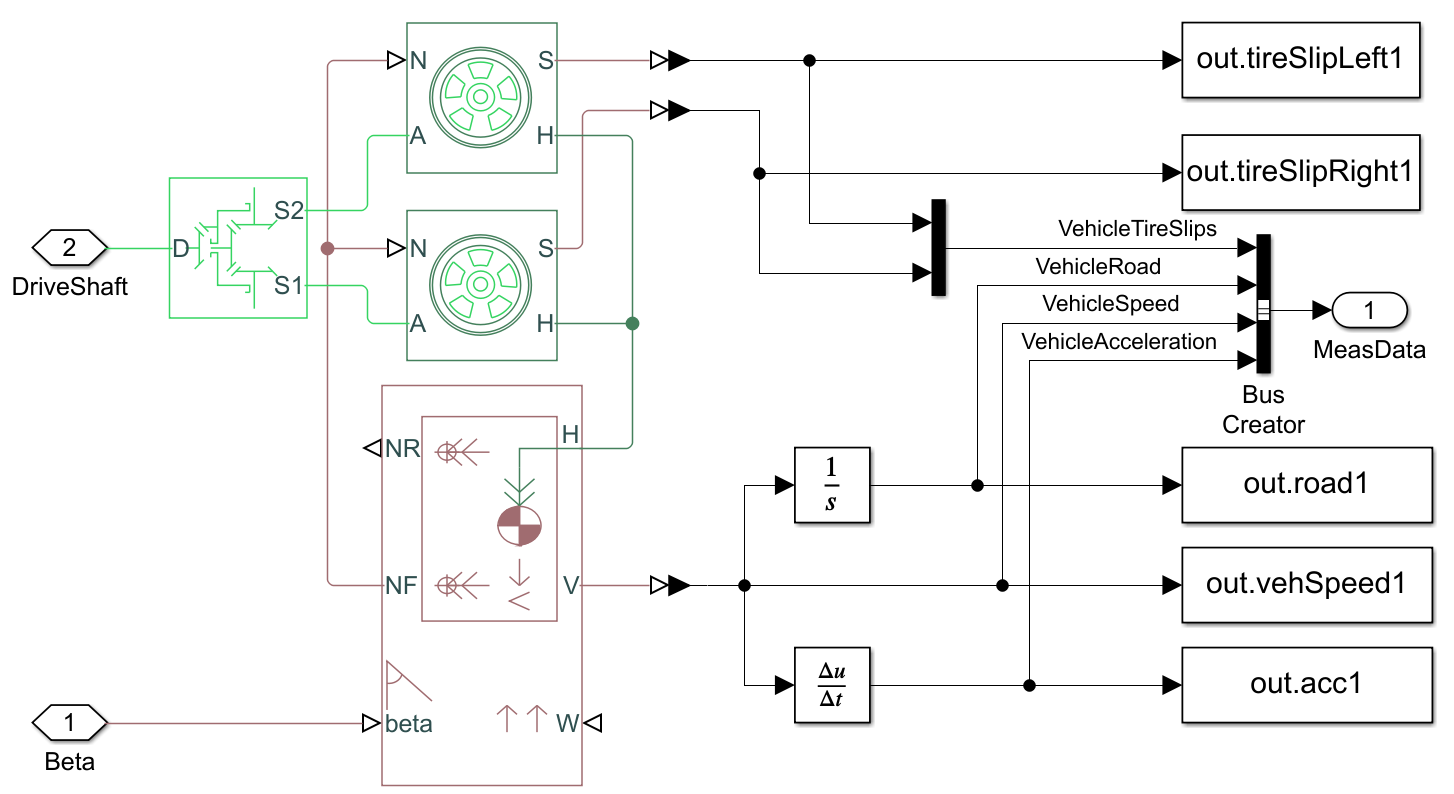
Jármű dinamika mérésére szolgáló modell

Adatforrások

A cél egy olyan eljárás kidolgozása, mely nem igényli, hogy szenzorok kerüljenek felszerelésre a járműre, viszont a jármű belső paraméterein túl a környezet és az útvonal jellemzőit is figyelembe veszi. Az előzmény kutatás során elsősorban buszokkal kezdtünk el foglalkozni, ezért eleinte forgalomban buszjáratokról kezdtünk menetciklusokat gyűjteni és ha szituáció engedte, akkor kamerával rögzítettük is az útvonalat, hogy a menetciklusban felfedezhető változások okai is dokumentálásra kerülhessenek. Később ezek kiegészültek távolsági járatokkal, majd személygépjárműves közlekedéssel.

Az útvonal által érintett domborzat magasságadatai alapján becslés tehető a következő útszakasz nyomatékigényére, ezért az útvonal terv ismeretében érdemes ezek begyűjtése is, melyeket online térképadatbázisokból sikerült beszerezni.

Mérések

Útvonalak rögzítése

A GPS Logger nevezetű Android alkalmazás GPX fájlokba gyűjti az útvonal adatait. A GPX egy XML formátumú szöveges állomány, melybe listaszerűen kerülnek felvévtelre az újabb és újabb adatpontok. A következő adatok kerülnek rögzítésre:

• GPS koordináták (latitude és longitude)
• Eleváció (méterben megadva)
• Időpont
• Pillanatnyi sebesség (méter/másodpercben megadva)
• Látható műholdak száma

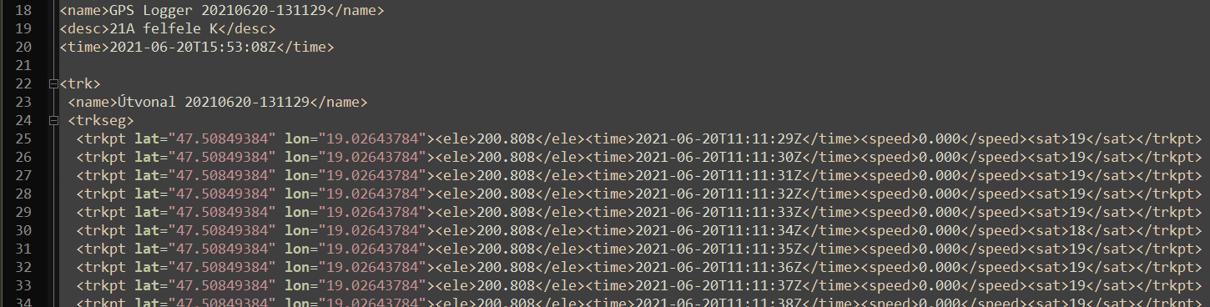
GPX állomány felépítése

Adatpontok közötti távolság meghatározása

Adatpont párokra ismételten alkalmazott Haversine-formula segítségével megkapható a gömbfelszínen haladó útvonal törtvonalas ábrázolása.

\[ \begin{equation} \label{haversine} \begin{gathered} a=\sin^2{\left(\frac{\Delta\phi}{2}\right)}+\cos{\left(\phi_1\right)}\cdot\cos{\left(\phi_2\right)}\cdot\sin^2{\left(\frac{\Delta\lambda}{2}\right)} \\ c=2\cdot{\mathrm{atan}}_2\left(\sqrt{a},\sqrt{1-a}\right) \\ d_{sp}=R\cdot \end{gathered} \end{equation} \] ahol

• \( \phi \): latitude (radiánban megadva),
• \( \lambda \): longitude (radiánban megadva),
• \( a \): két koordinátát összekötő húr hossza felének a négyzete,
• \( c \): szögtávolság (radiánban megadva),
• \( R \): Föld sugara (\( 6.371 \cdot 10^6 \textrm{ m}\)),
• \( d_{sp} \): gömbfelszínen vett távolság.

Ezt az adatsort a későbbiekben sebesség-idő függvénnyé kell alakítani.

Interpoláció

Átalakítás előtt érdemes átfésülni az adatsort, hogy tartalmaz-e hiányosságokat vagy olyan megállásokat (azaz \( 0 \frac{m}{s^2} \) értékeket), melyek hirtelen következtek be, tehát valószínűtlenek. Az ilyen kimaradásokat interpolációval ki lehet pótolni.

\[ \overline{v_{new}} = \overline{a_i} \cdot (t_{new} - t_i) + \overline{v_i} \] ahol

• \( \overline{v_{new}} \): a generált sebességérték,
• \( \overline{a_i} \): a két adatpont között állandónak tekintett gyorsulás,
• \( t_{new} \): az időpont melyhez az új sebességadat kerül hozzárendelésre,
• \( t_i \): a korábbi időpont, melyhez hozzá van rendelve sebssségérték,
• \( \overline{v_i} \): az ismert sebsségérték.

Adatsorok aggregálása

A szenzoros sebességmérés adatsora közvetlenül használható lenne, ha ismert lenne a szenzorok típusjelei, így az adatlapjukból kikereshető lenne a mérési hibájuk. Viszont ez az információ nem áll rendelkezésre. A gömbfelszínen vett távolságok adatsorából származó sebesség-idő függvény és a szenzoradatok által felvázolt sebesség-idő függvényeket aggregálva az adatsorok hibás méréseinek egy jelentő része kihullik, így az adatsor már közelebb áll a használható állapothoz.

Erre a célra a geometriai és harmonikus középértékek alkalmasak, ugyanis ezek szorzást alkalmaznak a két összevonni kívánt érték között, így ha az egyikben megállás szerepel, akkor a másik esetleges apró mozgása korrigálásra kerül. Ez a hiba jellemzően a GPS-es adatsort jellemzi.

\[ \overline{v_{geo}} = \sqrt{\overline{v_{calc}} \cdot \overline{v_{meas}}} \] \[ \overline{v_{harmonic}} = \frac{2 \cdot \overline{v_{calc}} \cdot \overline{v_{meas}}}{\overline{v_{calc}} + \overline{v_{meas}}} \] ahol

• \( \overline{v_{calc}} \): GPS adatokból számított sebességérték,
• \( \overline{v_{meas}} \): szenzoradatos sebességérték,
• \( \overline{v_{geo}} \): számított geometriai középérték,
• \( \overline{v_{harmonic}} \): számított harmonikus középérték.

Sebsség-idő és a Gyorsulás-idő függvény felvétele

A gömbfelszínen vett távolságok sorozatának időszerinti deriválásával megkapható az átlagsebességek sorozata, majd ismételt deriválás után a gyorsulások sorozata:

\[ \begin{equation} \begin{gathered} \overset{\left(N\left({d_{sp}}_n\right)-1\right)}{\underset{i=1}{v_n}} = \frac{{d_{sp}}_{(i+1)}-{d_{sp}}_i}{\textrm{dt}} \\ \overset{\left(N\left(\overline{v_n}\right)-1\right)}{\underset{i=1}{a_n}} = \frac{\overline{v_{(i+1)}}-\overline{v_i}}{\textrm{dt}} \end{gathered} \end{equation} \] ahol

• \( N(x_n) \): sor elemeinek száma,
• \( {d_{sp}}_n \): gömbfelszínen vett távolságok sora,
• \( {d_{sp}}_i \): gömbfelszínen vett távolságok sorának \( i \). eleme,
• \( \overline{v_n} \): sebesség értékek sora,
• \( \overline{v_i} \): sebesség értékek sorának \( i \). eleme,
• \( \overline{a_n} \): gyorsulás értékek sora.

Megfigyelhető, hogy meghatározásra került alsó és felső limit a sorozatok megadásakor. Ennek egyik oka, hogy a mérések az utazás végével lezárultak, tehát az adatpontok sokasága egy pozitív egész szám, ami elemszám után már nincs több adatpont; a másik oka, ami miatt az 1-es index és a -1 limit is hangsúlyozásra kerül az az, hogy végig különbségekkel kell számolni, így minden lépés után egyel kevesebb eleme lesz az újabb és újabb sorozatoknak. A gyorsulások sorozatának elemszáma így 3-mal kevesebb, mint a mért adatsor elemszáma.

Hihetőségi vizsgálat

Utasvédelmi okokból a gyorsulás nem lehet több, mint \( 2 \frac{m}{s^2} \). Miután a gyorsulások adatsora előállításra került, így esetszétválasztással már megmondható, hogy a gyorsulás időpontjához tartozó adatpont hihető adat vagy sem.

\[ \begin{equation} P_{test}(a_i) = \begin{cases} \textrm{plausible} & \textrm{if $a_i \leq 2 \frac{m}{s^2}$} \\ \textrm{implausible} & \textrm{if $a_i > 2 \frac{m}{s^2}$} \end{cases} \end{equation} \] ahol

• \( P_{test}(x) \): teszfüggvény,
• \( \overline{a_i} \): gyorsulás értékek sorának \( i \). eleme.

Eredmények grafikus megjelenítése

A fentebb tárgyalt algoritmus eredménye az alábbi ábrán látható menetciklus, melyhez még a magasságadatok változása is megfigyelhető.

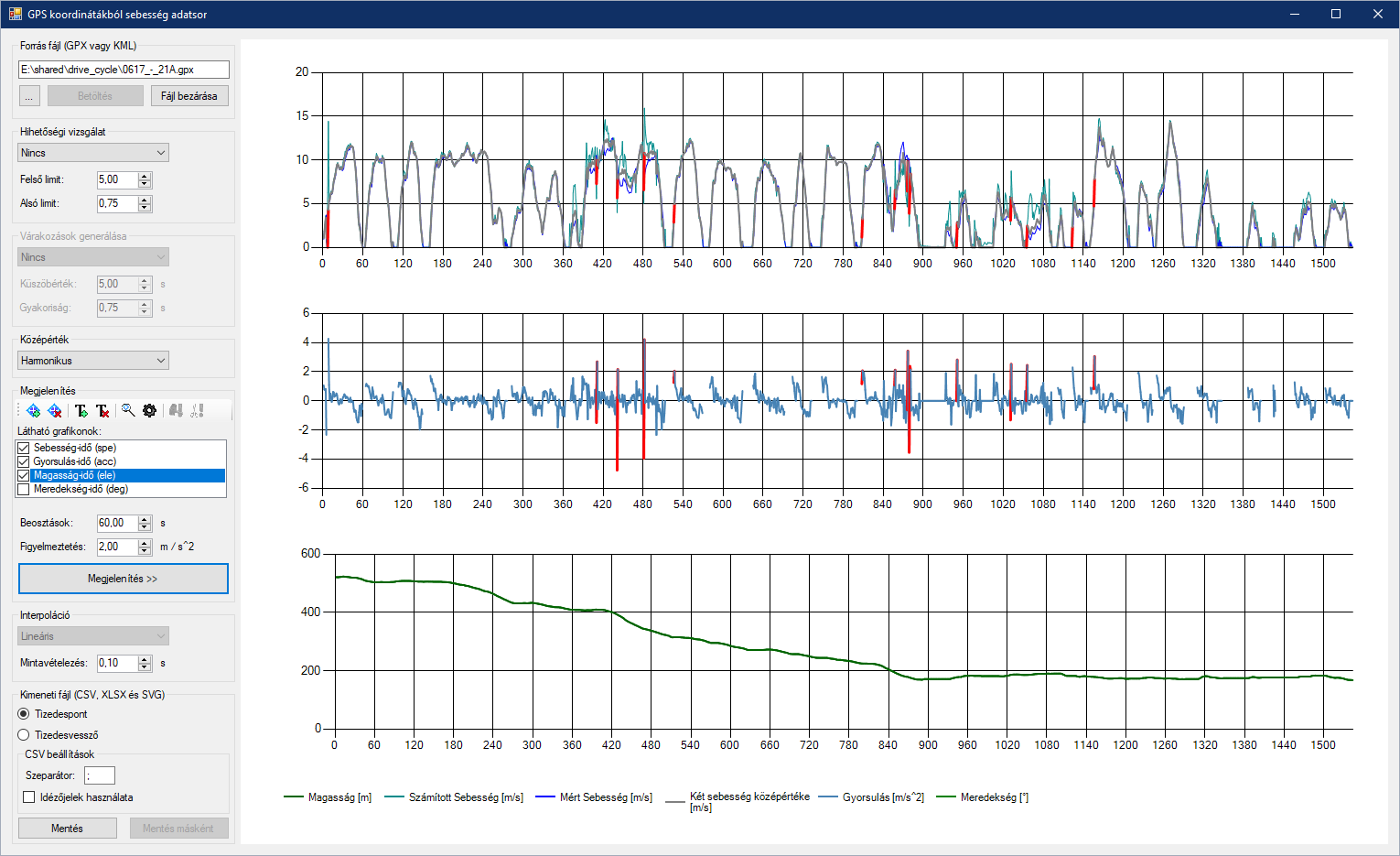
Eredmény (21A buszjárat)

Szintén a gyűjtött adatokból kiemelhető maga az útvonal, melyen a mérés készült. A magasságadatok és a koordináták egyértelműen meghatároznak a térben egy pontot, így 3D térben árázolható az utazás útvonala is.

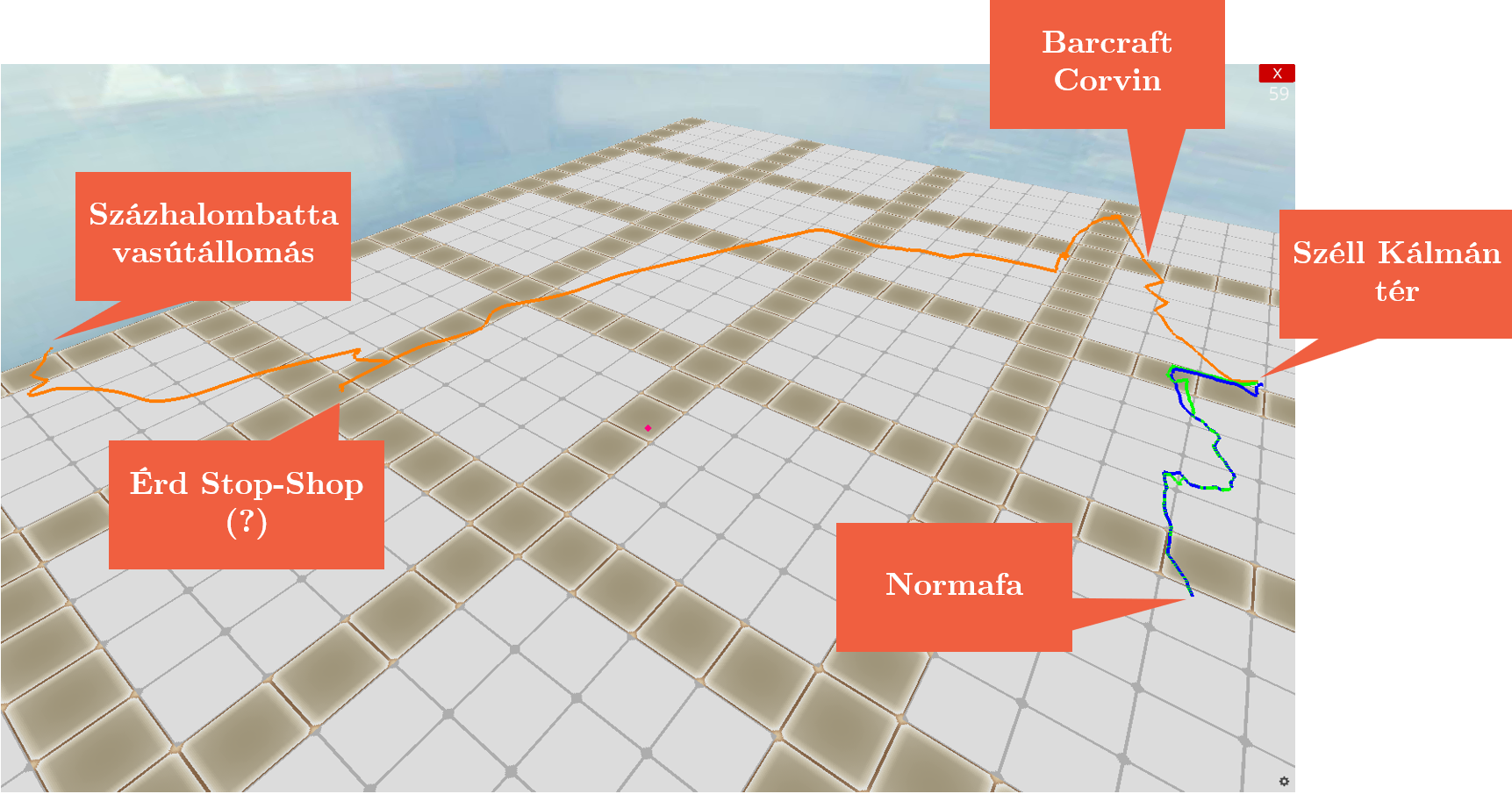
A 3D-s görbe kirajzolja a térben a megtett útvonalat

Adatbázisok

Domborzat adatainak beszerzése

Több online és offline adatforrás került felhasználásra a domborzat adatainak beszerzéséhez.

Az elevációs adatok a Global Multi-resolution Terrain Elevation Data (GMTED2010) forrásból származnak, a FID:30, Extent:30,0,50,30 jelű területegység foglalja magába hazánkat. Az adatcsomag az alábbi képen figyelhető meg képszerkesztővel elvégzett invertálás, fényesség és kontraszt beállítás után.

Műholdas domborzati kép, mint adatforrás

A `rasterio` nevet viselő python modulba betöltés után az eredeti adatforrás megjeleníthető spektrális ábraként.

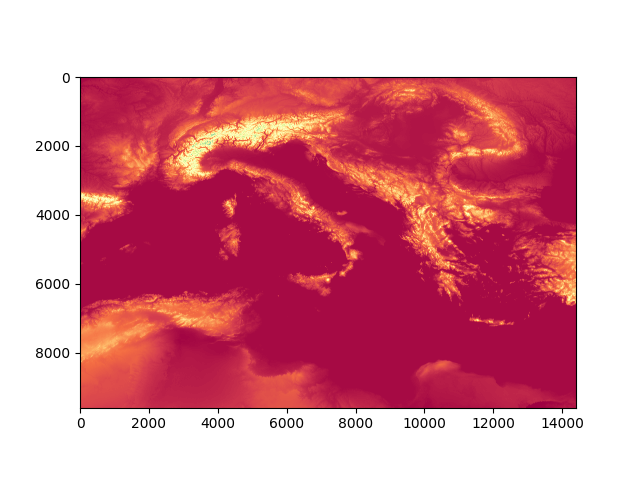
Domborzati adatok megjelenítve spektrális ábraként

A NaturalEarth oldaláról beszerzhetőek az orsázgok `.shp` fájljai. Az adminisztratív régió is innen származik, melynek segítéségével a nyers adatcsomagból kiemelhetőek a vizsgálni kívánt ország adatai.

Magyarország adminisztratív régiójával kivágva és felnagyítva

Egy színskála felállítása után a magasságadatokhoz színeket rendelhetünk, ezzel megkapható a 3 dimenziós modellehz használt textúra.

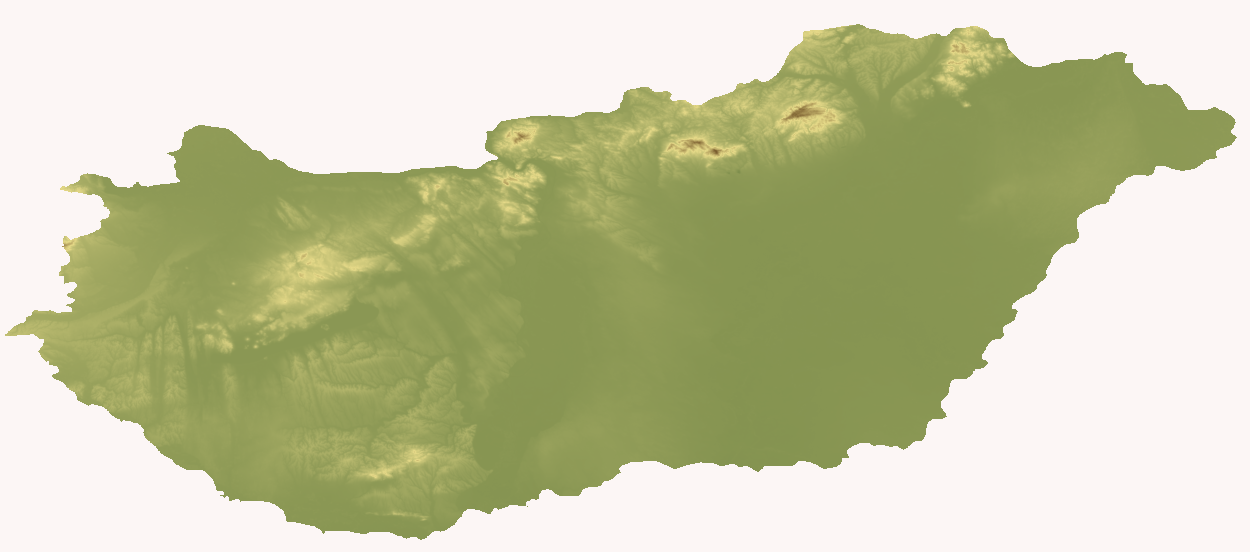
Domborzati színezet a magassági adatokból számítva

Egy sík felület felosztása után vertexei-t elmozgatva a magasságadatokal egy domborzati modell `Terrain` kapható. Erre a modellre kerül projektálásra a textúra.

Az OpenStreetMap adatbázisából az Overpass API-n keresztül kerül lekérdezésre a vízhálózat pontfelhője. Az ebből generált 3 dimenziós modell nem vesz részt az algoritmus működésében, csak támpontként szolgál a tájékozódáshoz a demonstrációs környezetben.

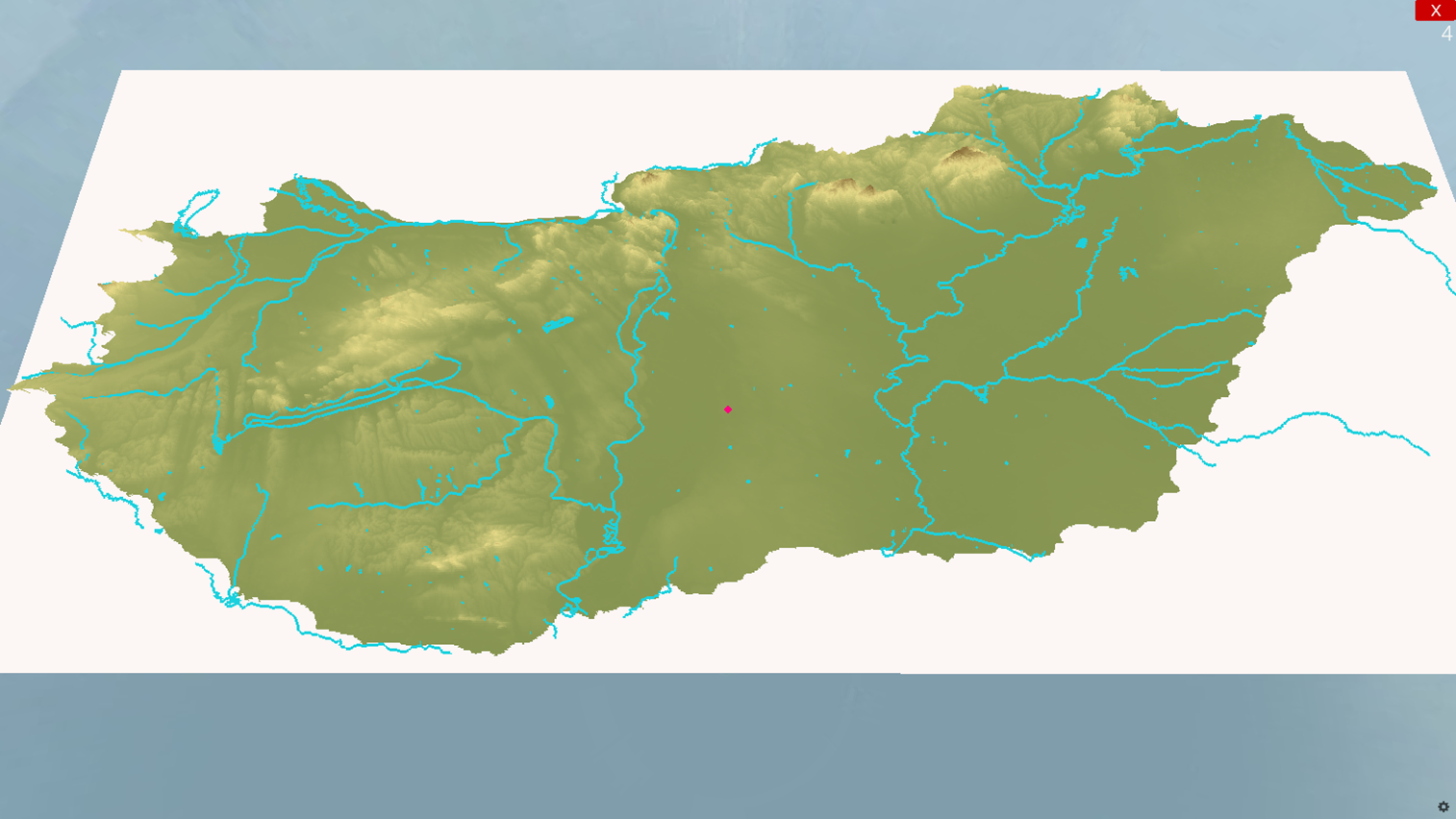
3D modell generálva, vízhálózattal együtt Ursina motorba betöltve

Keresőablak

Az útvonalak és a domborzati adatok beszerzése után a következő lépés, hogy az algoritmus hozzáférhessen ezeknek az adatoknak azon részeihez (lehetőleg már feldolgozva), melyekre éppen szüksége van. Ezt a célt szolgálja a bevezetett keresőablak.

Forma és felépítés

\[ \begin{equation} \mu_\tilde{X}(x) = \begin{cases} \frac{x-a_1}{a_2-a_1}, & \textrm{if $a_1 \lt x \lt a_2$} \\ 1, & \textrm{if $a_2 \leq x \leq a_3$} \\ \frac{a_4-x}{a_4-a_3}, & \textrm{if $a_3 \lt x \lt a_4$} \\ 0, & \textrm{otherwise} \end{cases} \end{equation} \] \[ \mu_\tilde{X}(x) = \max{\left( \min{\left( \frac{x-a_1}{a_2-a_1},1,\frac{a_4-x}{a_4-a_3} \right) },0 \right) } \]

Trapezoid típusú tagsági függvény

Trapézfüggvény előállítása trapezoid tagsági függvényből

Kereszteződések megjelenítése

Ideális kereszteződés a keresőablakban

Diagonális kereszteződés a keresőablakban

Lehetséges kanyarívek `1100` és `1110` kihajtási pontokhoz 1 kontrollpont segítségével ábrázolva

Kihajtás adatai

\[ \begin{equation} \mu_\tilde{X}(x) = \begin{cases} \frac{a_2-x}{a_2-a_1}, & \textrm{if $a_1 \lt x \lt a_2$} \\ 0, & \textrm{if $a_2 \leq x \leq a_3$} \\ \frac{x-a_3}{a_4-a_3}, & \textrm{if $a_3 \lt x \lt a_4$} \\ 1, & \textrm{otherwise} \end{cases} \end{equation} \]

V típusú tagsági függvény

X Kihajtási halmaz és néhány csomópont saját halmazának tagsági függvénye

Szintkülönbségek

Keresőablak a belső- (kihajtási) és a külső (szintmagasságok) kereteivel

Mesterséges intelligencia

Az oldal tartalmának feltöltése folyamatban van.
Kérem látogasson vissza később!

Megerősítéses tanítás

Ágens: Cselekvő és Kritizáló viszonya

Felhasznált irodalom

Dokumentumok

1. Dr. Simonyi Sandor: Gépjármű automata sebességváltók
2. Koczy T. László, Tikk Domonkos, Botzheim János: Intelligens rendszerek 2007.
3. Surin Sheth, Bhavya R. Gajjar, Purvi Chauhan: A Scope and Study of Automatic Transmission System in Context of Operating Parameter and Professional Requirement
4. Suyash Galgale, Prathamesh Deore, Ketan Pardeshi: Automobile Transmission Systems
5. Mahmoud Hamouda, Laszló Számel: Optimum Control Parameters of Switched Reluctance Motor for Torque Production Improvement over the Entire Speed Range
6. Muneeb Iftikhar: Fuel Cell
7. Umair Afzal, Haris Imtiaz, Abubakar Younis: PEM gaseous voltaic battery; Department of Electrical Engineering, University Of Gujrat, Hafiz Hayat Campus
8. John P. Kopasz, Theodore R. Krause, Shabbir Ahmed and Michael Krumpelt: Fuel requirements for fuel cell systems; Fuel Chemistry Division Preprints 2002, 47(2), 491
9. Shaharyar Yousaf: Comparison of Fuel Cell, Fuel Cell Battery, and Fuel Cell Ultra-Capacitor Vehicles; International Journal of Scientific & Engineering Research Volume 10, Issue 2, February-2019, ISSN 2229-5518
10. Antal Béla, Dollák Csaba, Kazai Imre: LG2212-T1 Tüzelőanyag cella mérési útmutató; BMF KKV VEI, Budapest, 2006. november
11. Dr. Molnár Kolos: Anyagismereti alapok; BME GPK PT, 2019.
12. Sztrókay Kálmán: Az atomkorszak; Tudomány 1946 február 3 szám
13. Dr. Rácz Ervin: Nukleáris Erőművek; ÓE-KVK 2119; Budapest 2015.
14. Mehrdad Ehsani, Yimin Gao, Sebastien E. Gay, Ali Emadi: Modern Electric, Hybrid Elecetric, and Fuel Cell Vehicles Fundamentals, Theory, and Design; CRC Press LLC, 2005; ISBN 0-8493-3154-4
15. C. Larouci, A. Chaibet and M. Boukhnifer: A Vehicle Transmission Simulator Applied to the Automated Driving; VTC Spring 2009 - IEEE 69th Vehicular Technology Conference, 2009, pp. 1-5, doi: 10.1109/VETECS.2009.5073353.
16. Masaaki Minakawa, Jun Nakahara, Jiro Ninomiya, Yukihiro Orimoto: Method for measuring force transmitted from road surface to tires and its applications; JSAE Review 20 (1999) 479-485; DOI:10.1016/S0389-4304(99)00054-5
17. Kovács Judit: Döntéspszichológiai laborgyakorlatok; Didakt; ISBN 978-615-5212-21-5
18. P. Y. Glorennec and L. Jouffe: Fuzzy Q-learning; Proceedings of 6th International Fuzzy Systems Conference, 1997, pp. 659-662 vol.2, doi: 10.1109/FUZZY.1997.622790.
19. A. Arya and K. Badie: A connectionist approach to reorganization of knowledge structures in fuzzy systems; Proceedings of 6th International Fuzzy Systems Conference, 1997, pp. 1075-1081 vol.2, doi: 10.1109/FUZZY.1997.622859.
20. J. Hollatz: A fuzzy advisory system for estimating the waiting period after traffic accidents; Proceedings of 6th International Fuzzy Systems Conference, 1997, pp. 1475-1479 vol.3, doi: 10.1109/FUZZY.1997.619761.
21. Xun Gong, Jayanth Rangaraju: Taking charge of electric vehicles - both in the vehicle and on the grid; Texas Instruments Incorporated
22. Narjes Kheirabadi, Azizollah Shafiekhani: Graphene/Li-ion battery; Journal of Applied Physics Volume 112, Issue 12 DOI:10.1063/1.4771923
23. Md Sohanur Rahman, Bapi Mondal, Md Masum Parvez, Aqib Adnan Shafin, Md. Mehedi Hasan, Bushra Saba, Istiuqe Ahmed, Md. Mahmud: Overview of Graphene as Promising Electrode Materials for Li-ion Battery; International Journal of Scientific Research and Engineering Development-– Volume 4 Issue 6, Nov-Dec 2021; ISSN 2581-7175
24. Gints Kucinskis, Gunars Bajars, Janis Kleperis: Graphene in lithium ion battery cathode materials: A review; Elsevier Journal of Power Sources 240 (2013) 66e79; DOI:10.1016/j.jpowsour.2013.03.160
25. Petrók János: A gépkocsi fékezési energiájának hasznosítása, Autótechnika 2009
26. Danielson, J.J., and Gesch, D.B., 2011, Global multi-resolution terrain elevation data 2010 (GMTED2010) - High resolution data source: U.S. Geological Survey Open-File Report 2011–1073, 26 p. DOI:10.5066/F7J38R2N
27. Surin Sheth, Bhavya R. Gajjar, Purvi Chauhan: A Scope and Study of Automatic Transmission System in Context of Operating Parameter and Professional Requirement; Conference Paper; February 2014; DOI: 10.13140/2.1.2729.0403
28. M Inalpolat and A Kahraman: Dynamic modelling of planetary gears of automatic transmissions; DOI: 10.1243/14644193JMBD138
29. Gáti József, Horváth Sándor: A Ford T-modell bolygóműves váltója, az automata váltók első előhírnöke; Óbuda University e‐Bulletin Vol. 1, No. 1, 2010
30. Suyash Galgale, Prathamesh Deore, Ketan Pardeshi: Automobile Transmission Systems; IJSRD - International Journal for Scientific Research & Development; Vol. 5, Issue 08, 2017; ISSN (online): 2321-0613
31. Dr. Bereczky, Ákos, Dr. Varga, Zoltán: Motor és erőátviteli rendszerek mechatronikája; 2014; ISBN 978-963-313-172-5
32. Byung-Kwan Shin, Jin-Oh Hahn, Kyongsu Yi, Kyo-II Lee: A Supervisor-Based Neural-Adaptive Shift Controller for Automatic Transmissions Considering Throttle Opening and Driving Load; KSME International Journal, VoL 14, No.4. pp. 418-425.2000
33. Deok-Ho Kim, Jin-Oh Hahn, Byung-Kwan Shin, Kyo-II Lee: Adaptive Compensation Control of Vehicle Automatic Transmissions for Smooth Shift Transients Based on Intelligent Supervisor; KSME International Journal; VoL 15 No. 11, pp. 1472-1481, 2001
34. Mahmoud Hamouda, László Számel: Optimum Control Parameters of Switched Reluctance Motor for Torque Production Improvement over the Entire Speed Range; Acta Polytechnica Hungarica Vol. 16, No. 3, 2019
35. Gabriella Kosztolányi-Iván, Csaba Koren, Attila Borsos: Can People Recognize More Than Six Road Categories?; Acta Polytechnica Hungarica Vol. 16, No. 6, 2019

Online források

1. MATLAB Foundations of Fuzzy Logic
2. MATLAB Defuzzification Methods
3. MATLAB trimf
4. MATLAB trapmf
5. Magyar Hidrogén és Tüzelőanyag-cella Egyesület – Tüzelőanyag-cellák
6. MVM Paksi Atomerőmű Tudástár – Atomtörténelem
7. Wikipedia Nuclear marine propulsion
8. Wikipedia Turbo-electric transmisison
9. X-engineer EV design -vehicle control modes
10. X-engineer Drivetrain losses efficiency
11. X-engineer Vehicle acceleration and maximum speed modeling and simulation
12. MATLAB Vehicle Body
13. Totalcar: Mi az az inverter?
14. Yngve Solbakken: Space Vector PWM Intro
15. X-engineer EV design – electric motor
16. Totalcar: Ezek az új villanymotorok már egészen másról szólnak
17. X-engineer EV design – battery simulation
18. X-engineer EV design – battery calculation
19. Wikipedia – Torque Vectoring
20. X-engineer – Why do we need gears
21. Totalcar: Ezért nincs a villanyautóknak sebességváltójuk
22. Wikipedia- Hans B. Pacejka
23. Cool-Mobil Kft.: ABS, ASR, ESP és A Többiek…
24. Schiller: Mi az ESP jelentése az autóknál, és hogyan működik?
25. hvg.hu: Három betű, ami segíthet megállni az autóval: így működik az EBD
26. Wikipedia: Kardáncsukló
27. MathWorks: Modeling a Four-Wheel Drive Powertrain
28. Towards Data Science: Creating Beautiful Topography Maps with Python
29. U.S. Geological Survey: GMTED2010
30. NaturalEarth: 1:10m Cultural Vectors
31. OpenStreetMap Wiki: Overpass API/Overpass QL
32. overpass turbo
33. Erős Márk: Mi az a CVT-váltó?
34. Movable Type Scripts: Calculate distance, bearing and more between Latitude/Longitude points
35. Nyquist Sampling Theorem